Course notes for “Stochastic Process”
2014 Fall
1. Motivation
Brownian motion can be thought of a symmetric random walk where the jumps sizes are very small and where jumps occur very frequently.
- Each jump size are
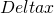
- The time before two jumps are
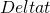 .
.
1.1 What’s the mean and variance?
Let
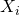
denote whether the i-th jump is to the right(+1) or to the left(-1), we have
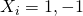
with probability
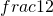
and
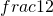
respectively.
Thus,
![Rendered by QuickLaTeX.com E[X_i] = 0](http://mytechroad.com/wp-content/ql-cache/quicklatex.com-f8aaebca6a792a3c1f96703c49cc3f67_l3.png)
and
![Rendered by QuickLaTeX.com Var[X_i] = E[X^2_i] - E[X_i]^2 = 1](http://mytechroad.com/wp-content/ql-cache/quicklatex.com-1b4a23e17c1ffe9311f56a51f18e7bb9_l3.png)
.
Let  denote the state of Markov Chain after n jumps, then
denote the state of Markov Chain after n jumps, then
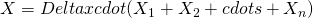
The 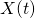 denote the continuous Markov Chain after n jumps, then
denote the continuous Markov Chain after n jumps, then
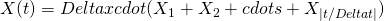
Then we have
![Rendered by QuickLaTeX.com E[X(t)] = 0](http://mytechroad.com/wp-content/ql-cache/quicklatex.com-5521d8e7a8c3e27e09dae171218efa5f_l3.png) and
and ![Rendered by QuickLaTeX.com Var[X(t)] = (Delta x)^2 cdot frac{t}{Delta t}](http://mytechroad.com/wp-content/ql-cache/quicklatex.com-0f44ab27f24a965379568a8548d9ea92_l3.png) .
.
Let 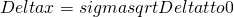 , then
, then
![Rendered by QuickLaTeX.com V[X(t)] = (Delta x)^2 cdot frac{t}{Delta} to sigma^2 t](http://mytechroad.com/wp-content/ql-cache/quicklatex.com-fb1f4cf9dd65e73704e883268ac9c80c_l3.png) .
.
2. Properties of Brownian Motion
Answer: by the stationary property, we have
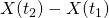
~
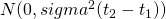
.
3. Standard Brownian Motion (SBM)
4. Brownian Motion with Drift
Definition 1: Let 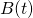 be the standard Brownian motion. Let
be the standard Brownian motion. Let 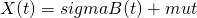 , then
, then 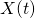 is Brownian motion with drift
is Brownian motion with drift 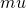 .
.
Definition 2: 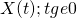 .
. 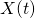 is Brownian Motion with drift
is Brownian Motion with drift 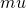 and variance parameter
and variance parameter 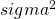 if
if
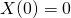
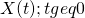 has stationary and independent increments
has stationary and independent increments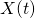 ~
~ 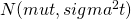
Example: Let 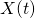 be Brownian motion with
be Brownian motion with 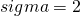 and drift
and drift 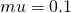 . What is
. What is 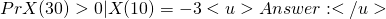 Pr{X(30) >0 | X(10) = -3}
Pr{X(30) >0 | X(10) = -3} Pr{X(30) – X(20) >3 | X(10) =3 }
Pr{X(30) – X(20) >3 | X(10) =3 } Pr{X(30) – X(10) >3 }
Pr{X(30) – X(10) >3 } Pr{X(20) – X(0) >3 }
Pr{X(20) – X(0) >3 } Pr{X(20)>3 }
Pr{X(20)>3 } Pr{N(2,80) > 3} = Pr{X(0,1) > frac{3-2}{sqrt{80}}
Pr{N(2,80) > 3} = Pr{X(0,1) > frac{3-2}{sqrt{80}} 1-Phi(frac{1}{4sqrt{5}})
1-Phi(frac{1}{4sqrt{5}})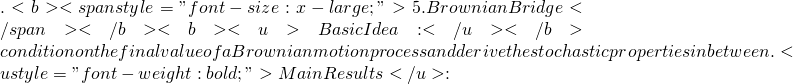 X(s) = x | X(t) = B
X(s) = x | X(t) = B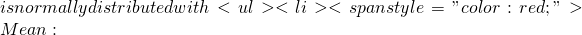 frac{s}{t} cdot B
frac{s}{t} cdot B frac{s}{t} cdot (t-s)
frac{s}{t} cdot (t-s) s = t/2
s = t/2 X(t)
X(t) N(0, sigma^2 t)
N(0, sigma^2 t)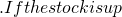 10 after 6 hours, what is the probability that the stack was above its starting value after 3 hours?
10 after 6 hours, what is the probability that the stack was above its starting value after 3 hours?
Answer:
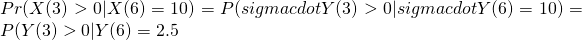
This is a Brownian bridge process where
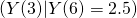
~
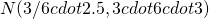
=
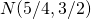
.
Thus
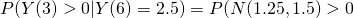
Example 2: If a bicycle race between two competitors, Let 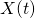 denote the amount of time (in seconds) by which the racer that started in the insider position is ahead when 100t percent of the race has been completed, and suppose that
denote the amount of time (in seconds) by which the racer that started in the insider position is ahead when 100t percent of the race has been completed, and suppose that 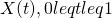 , can be effectively modeled as a Brownian Motion process with variance parameter
, can be effectively modeled as a Brownian Motion process with variance parameter 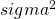 .
.
6. First Passage Time
Let 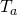 denote the first time that standard Brownian motion hits level a (starting at X(0) = 0), assuming a >0, then we have
denote the first time that standard Brownian motion hits level a (starting at X(0) = 0), assuming a >0, then we have
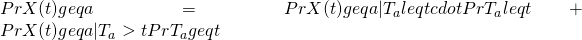
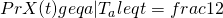 : you know that at some time before t, the process hits a. From that point forward, you are just as likely to be above a as below a.
: you know that at some time before t, the process hits a. From that point forward, you are just as likely to be above a as below a. 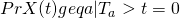 :
: 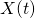 cannot be above a, because the first passage time to a is after t.
cannot be above a, because the first passage time to a is after t.
Thus,
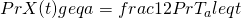
,
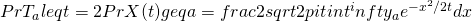
.
Change variables: 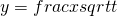 , we have
, we have 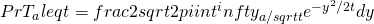 .
.
By symmetry, we get 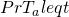 .
.
![]() on m possible outcomes:
on m possible outcomes: ![]() .
.![]() to be the outcome of wagers i if outcome j occurs.
to be the outcome of wagers i if outcome j occurs.![]() is bet on wager
is bet on wager ![]() , then
, then ![]() is earned if outcome j occurs.
is earned if outcome j occurs. such that
such that 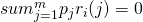 ,
, 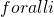
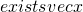 such that
such that 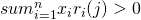

 X(s) = x | X(t) = B
X(s) = x | X(t) = B X(t)
X(t)