Compound Poisson Process (CPP)

Posted on by

1. Definition: 

Remove the restriction that two or more customers cannot arrive at the same time, (i.e., remove orderliness property)

Let 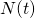N(t) be a Poisson Process with rate 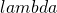lambda, and let 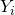Y_i be the i.i.d random variable, then 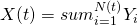X(t) = sum^{N(t)}_{i=1} Y_i is a compound Poisson process

Example #1: Buses arrive according to a Poisson process. Let 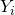Y_i be the number of people on bus i, and let 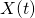X(t) be the total number of people arriving by time t.

Example #2: Insurance claims arrive according to a Poisson process. Let 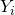Y_i be the size of the claim (in dollars), and let 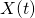X(t) be the total amount due to all claims by time t.

2. Expectation: 

E[X(t)] = E[E[X(t)|N(t)]]
Since E[X(t)|N(t) = n] = E[sum^n_{i=1} Y_i] = nE[Y_i], i.e., E[X(t)|N(t)] = N(t)E[Y_i]
So E[E[X(t)|N(t)]] = E[N(t)E[Y_i]] = E[N(t)]*E[Y_i] = lambda t E[Y_i]

3. Variance: 

var[X(t)] = var[E[X(t)|N(t)]] + E[var[X(t)|N(t)]]
and we have Var[X(t)|N(t)=n] = var(sum^n_{i=1} E[Y_i]) = nVar[Y_i]
or var(X(t)|N(t)) = N(t)Var(Y_i).
So Var[E[X(t)|N(t)]] + E[Var[X(t)|N(t)]]
  = Var[N(t)E(Y_i)] + E[N(t)Var[Y_i)]
  = lambda t E^2[Y_i] + lambda t Var(Y_i)
  = lambda t E^2[Y_i] + lambda t (E[(Y_i)^2] - E^2[Y_i])
  = lambda t E[(Y_i)^2]

4. Example: 



Leave a Reply