Excess Distribution of Renewal Process
– Course notes of Stochastic Process, 2014 Fall
1. Definition
Excess of renewal process is defined as 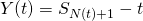 (time until next event)
(time until next event)
In the example of average time waiting bus, we drived
Now we are going to derive ![]() for a random
for a random ![]() .
.
Interpretation: You show up “at random”. What is the probability that you wait more than x for the next event?
2. Derivation of 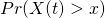
As we want to determine the fraction of time that 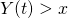 .
.
Let 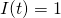 if
if 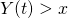 , and let
, and let 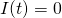 otherwise.
otherwise.
Interpretation: Fraction of time that 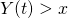 = Fraction of “on” time for
= Fraction of “on” time for 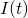
Let 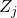 be “on” time during cycle
be “on” time during cycle 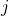 , then
, then 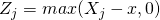
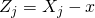 if
if 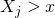
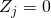 otherwise
otherwise
Note: the ON time and OFF time for each cycle are dependent. A longer ON time implies a shorter OFF time.
Then we have
= 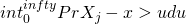
= 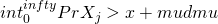
= 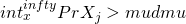
Since 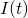 is an alternating renewal process, fraction of “on” time is
is an alternating renewal process, fraction of “on” time is
This is sometimes called equilibrium distribution,
3. Example of different distribution of 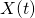
Example: 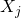 ~ exp
~ exp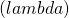
= 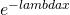
As expected (by memoryless property), excess distribution is an exponential distribution.
Example: Pareto Distribution
Some properties: ![Rendered by QuickLaTeX.com E[X_j ] = frac{1}{alpha}](http://mytechroad.com/wp-content/ql-cache/quicklatex.com-227d4cb85491bbc153e8a45a7d34074a_l3.png) (mean only exist if
(mean only exist if 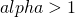
Example: Deterministic 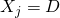
– Assume 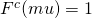 if
if 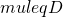 , otherwise
, otherwise 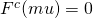 .
.
= 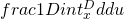
= 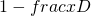
This is the CCDF of a uniform distribution on ![Rendered by QuickLaTeX.com [0,D]](http://mytechroad.com/wp-content/ql-cache/quicklatex.com-d4e9347560fc995f60d5b13526ac2e73_l3.png) .
.
Note: the above assume that 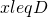 , If
, If 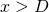 , then the result is 0.
, then the result is 0.
