Exponential Distribution and Properties

– Stochastic Process course notes

1. Definition

Probability function: $f(x) = lambda e^{-lambda x}$ , $x geq 0$
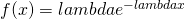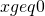
Cumulative Distribution Function (CDF): $F(x) = 1-e^{-lambda x}$ , $x geq 0$
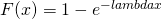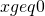
Complement of the CDF (CCDF): $F^c(x) = e^{-lambda x}$ , $x geq 0$ .

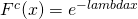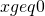2. Memoryless Property

Def`1: A random variable X has the memoryless property if 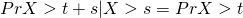$Pr{X>t+s| X>s} = Pr{X>t}$

Def`2: A random variable X has the memoryless property if $Pr{X>t+s} = Pr{X>t} Pr{X>s}$

The exponential distribution is the only distribution that has the memoryless property (Satisfy definition 2)

3. Useful Properties: First occurrence among events

Assume $X_1, X_2, cdots, X_n$ are exponential variable with rate $lambda_1, lambda_2, cdots, lambda_n$ .
Then what is the probability that $X_1 < X_2$ .

More generally

$Pr{X_i = min[X_1,cdots, X_n]} = frac{lambda_i}{lambda_1+lambda_2+cdots +lambda_n}$

4. Distribution of time of first event

This is the CDF of an exponential RV with rate 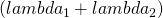$(lambda_1 + lambda_2)$ , therefore

$min(X_1, X_2)$ ~ $exp(lambda_1 + lambda_2)$

Lisa Tech Blog

My security road