Association Rule Mining

Posted on by

1. Definition

  • Association: Given a set of transactions, find rules that will predict the occurrence of an item based on the occurrence of other items in the transaction. 
  • Support count (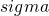sigma): frequency of occurrence of an itemset
  • Support: fraction of transactions that contain an item set
  • Frequent Itemset: An itemset whose support is greater or equal to a minsup threshold
2. Association rule
  • Association rule
    • </span> </b>X rightarrow Y
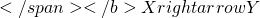
  • support (s)
    • fraction of transactions that contains both X and Y
  • confidence
    • measures how often items in Y appear in transactions that contains X
3. Association Rule Mining Task

  • Given a set of transactions T, the goal of association rule mining is to find all rules having 
    • support >= minsup threshold
    • confidence >= minconf threshold
  • Brute-force approach
    • list all possible association rules
    • compute the support and confidence for each rule
    • prune rules that fail the minsup and minconf thresholds
    • this is computationally prohibitive!
4. Two-step Approach
  • Step 1: frequent itemset generation
    • generate all itemset whose support >= minsup
  • Step 2: rule generation
    • generate high confidence rules from each frequent itemset, where each rule is a binary partitioning of a frequent itemset
  • Drawback: frequent itemset generation is still computationally expensive
5. Computational Complexity
  • Given d unique items
    • total number of item set is: 2^d
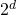
    • total number of possible association rules is:
    •  R = sum^{d-1}_{k=1} [binom{d}{k} *sum^{d-k}_{j=1}binom{d-k}{j}] = 3^d - s^{d+1} +1
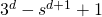
6. Reducing Number of Candidates
  • Apriori principal
    • If an itemset is frequent, then all of its subsets must also be frequent
    • i.e., forall X, Y: X subset Y rightarrow S(X) geq S(Y)
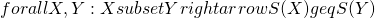
  • Apriori algorithm
    • Let k = 1
    • generate frequent itemset of length 1
    • repeat until no new frequent itemsets are identified
      • generate length (k+1) candidate itemsets from length k frequent itemsets
      • prune candidate itemsets containing subsets of length k that are infrequent 
      • count the support of each candidate by scanning the db
      • eliminate candidates that are infrequent, leaving only those that are frequent
7. Closed Itermset

  • An itemset is closed if none of its immediate supersets has the same support as the itemset.
8. Effect of Support Distribution
  • How to set the appropriate minsup threshold?
    • if minsup is set too high, we could miss items involving interesting rate items (e.g., expensive products)
    • if minsup is set too low, it is computatinally expensive and the number of itemset is very large.
  • Using a single minimum support threshold may not be effective.

Leave a Reply