Lemma
[1] Consider a process that throws balls uniformly at random into b bins and let C be a subset of these bins. If the process throws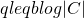 
balls, then the probability that each bin in C has at least one ball is at most 
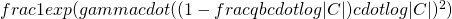if 
, where 
is some constant strictly less than 1. If 
, then the probability is at most 
.
balls, then the probability that each bin in C has at least one ball is at most if 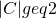, where 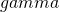is some constant strictly less than 1. If 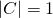, then the probability is at most .
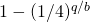Comment: conpon analysis + chernoff bound
Lemma
[1] Consider a process that throws t balls into b bins uniformly at random. if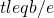 
, then the probability that there are at most 
occupied bins is at most 
.
, then the probability that there are at most 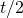occupied bins is at most 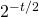.Lemma
[1] Consider a process that throws balls uniformly at random into b bins and let C be a subset of these bins. If the process throws q balls, then the probability that at least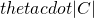 
of the bins in 
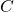have at least one ball is at most 
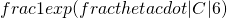if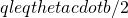 
; and at most 
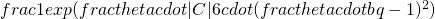if 
.
of the bins in have at least one ball is at most if ; and at most if 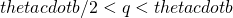. Reference
[1] Co-Location-Resistant Clouds, by Yossi Azar et al. in CCSW 2014