Introduction
- VCG can maximize the social welfare given the individuals are all “selfish”
Model
- Players
- There are
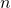 game players,
game players, 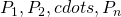
- Actions
- The actions of the players are denoted as
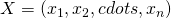
- Payoff
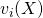
- Real demand
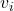
- Cost
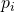 for its action
for its action- Utility
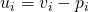
Definition
Following Nisan’s work, the terms “mechanisms” and “incentive compatible” are defined as
Mechanism
- Given a set of n players, and a set of outcomes, A, let
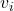 be the set of possible valuation functions of the form
be the set of possible valuation functions of the form 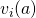 which player
which player 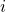 could have for an outcome
could have for an outcome 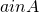 . A mechanism is a function
. A mechanism is a function 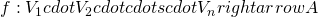 . Given the evaluations claimed by the players, f selects an outcome, and n payment functions,
. Given the evaluations claimed by the players, f selects an outcome, and n payment functions, 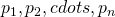 , where
, where 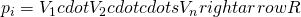 .
.
The above defines Action and Reward.
Incentive Compatible
- For every player
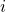 , every
, every 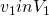 ,
, 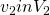 ,
, 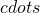 ,
, 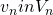 , and every
, and every 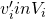 , where
, where 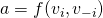 and
and 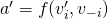 , then
, then 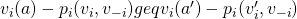 , then the mechanism is incentive compatible.
, then the mechanism is incentive compatible.
Specifically, among those incentive compatible mechanisms, the Vickrey-Clarke-Groves (VCG) mechanism is the mostly used one.
The VCG generally seeks to maximize the social welfare of all players in one game, where the social welfare is calculated as 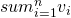 . So the goal function of VCG is
. So the goal function of VCG is 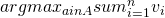 .
.
The VCG mechanism and the rule to design VCG mechanisms are defined as follows.
VCG Mechanism
- A mechanism, consisting of payment functions
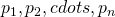 and a function
and a function 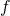 , for a game with outcome set
, for a game with outcome set 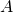 , is a Vickrey-Clarke-Groves mechanism if
, is a Vickrey-Clarke-Groves mechanism if 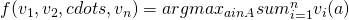 ( f maximizes the social walfare) for some functions
( f maximizes the social walfare) for some functions 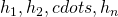 , where
, where 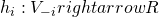 (h_i does not depend on
(h_i does not depend on 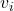 )
) 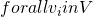 ,
, 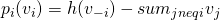 .
.
My understanding
- For user
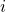 , its reward is depended on others, and not related to its action
, its reward is depended on others, and not related to its action - But why in the payment function, it deducts other users’ true value?
Clarke Pivot Rule
- The choice
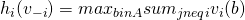 is called the Clark pivot payment. Under this rule the payment of player
is called the Clark pivot payment. Under this rule the payment of player 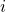 is
is 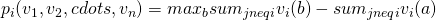 where
where 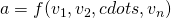 .
.
My understanding
- I didn’t understand it yet.
