1. Notation
- M: “Markovian” or “Memoryless” arrival process (i.e., Poisson Process)
- G: General service time (not necessarily exponential)
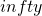 : Infinite number of servers
: Infinite number of servers
Let
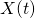 be the number of customers who have completed service by time t
be the number of customers who have completed service by time t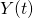 be the number of customers who are being served at time t
be the number of customers who are being served at time t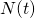 be the total number of customers who have arrived by time t
be the total number of customers who have arrived by time t
2. Splitting the arrival process
- Fix a reference time T.
- Consider the process of customers arriving prior to time T.
- A customer arriving at time
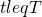 is
is - Type I: if service is completed before T
- occur with probability
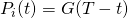
- Type-II: if customer still is service at time T
- occur with probability
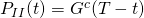
Since arrival times and services times are all independent, the type assignments are independent. Therefore,
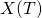 is a Poisson random variable with mean
is a Poisson random variable with mean 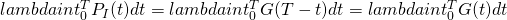 .
.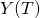 is a Poisson random variable with mean
is a Poisson random variable with mean 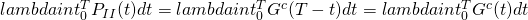
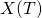 and
and 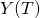 are independent
are independent
What happens when 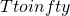
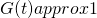 for large t. Therefore,
for large t. Therefore, 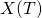 is a Poisson random variable with mean
is a Poisson random variable with mean 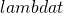
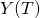 is a Poisson random variable with mean
is a Poisson random variable with mean ![Rendered by QuickLaTeX.com lambda int^T_0 G^ct)dt = lambda E[G]](http://mytechroad.com/wp-content/ql-cache/quicklatex.com-2c5d36fa13d7d0d546ab1022413e9709_l3.png)
Summary: Number of customers in service in an 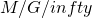 queue, in steady state, is a Poisson random variable with mean
queue, in steady state, is a Poisson random variable with mean ![Rendered by QuickLaTeX.com lambda E[G]](http://mytechroad.com/wp-content/ql-cache/quicklatex.com-733d417309a30bc479f8632158db9591_l3.png) .
.
