1. Bargaining problems Scenarios
Bargaining problems represent situations in which
- There is a conflict of interest about agreements.
- Individual have the possibility of concluding a mutually beneficial agreements.
- No agreement may be imposed on any individual without his approval
2. Bargaining problem Definition
Example: Suppose 2 players must split one unit of good. If no agreement is reached, then players do not receive anything. We define the following notations.
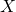 : the set of possible agreements
: the set of possible agreements- X = {
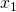 ,
, 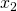 )|
)| 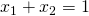 ,
, 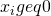 }
} 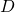 : the disagreement outcome
: the disagreement outcome- D = (0,0)
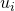 : each player i has preferences, represented by a utility function
: each player i has preferences, represented by a utility function 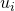 over
over 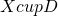
Definition: a bargaining problem is then defined as a pair of 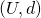 where
where 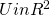 and
and 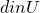 . We assume that
. We assume that
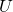 is a convex and compact set
is a convex and compact set- There exists some
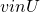 such that
such that 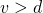 (i.e.,
(i.e., 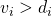 for some i)
for some i)
3. Axioms
- Pareto Efficiency
- A bargaining solution
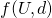 is Pareto efficient if there does not exist a
is Pareto efficient if there does not exist a 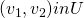 such that
such that 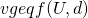 and
and 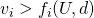 for some
for some 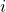 .
. - An inefficient outcome is unlikely, since it leaves space for renegotiation.
- Symmetry
- Let
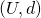 be such that
be such that 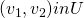 if and only if
if and only if 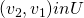 and
and 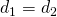 . Then
. Then 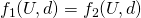 .
. - If the players are indistinguishable, the agreement should not discriminate between them.
- Invariance to Equivalent Payoff Representations
- Given a bargaining problem
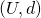 , consider a different bargaining problem
, consider a different bargaining problem 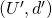 , for some
, for some 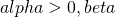 .
. 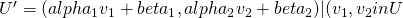
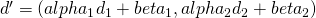
- Then
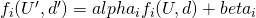
- Utility functions are only representation of preferences over outcomes. A transformation of the utility function that maintaining the same ordering over preferences (such as linear transformation) should not alter the outcome of bargaining process.
- Independence of Irrelevant Alternatives
- Let
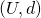 and
and 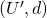 be two bargaining problems such that
be two bargaining problems such that 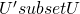 , if
, if 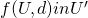 , then
, then 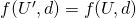 .
.
4. Nash Bargaining Solution
Definition: We say that a pair of payoffs ![]() is a Nash bargaining solution if it solves the following optimization problem
is a Nash bargaining solution if it solves the following optimization problem
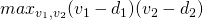
- subject to
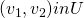
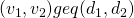
We use 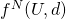 to denote the Nash Bargaining Solution
to denote the Nash Bargaining Solution
Remarks:
- Existence of an optimal solution: since the set
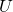 is compact and the objective function of the problem is continuous, there exists an optimal solution for the problem
is compact and the objective function of the problem is continuous, there exists an optimal solution for the problem - Uniqueness of the optimal solution: the objective function of the problem is strictly quasi-concave. Therefore, the problem has a unique solution.
Proposition: Nash bargaining solution ![]() is the unique bargaining solution that satisfies the 4 axioms.
is the unique bargaining solution that satisfies the 4 axioms.
Reference
[1] Game Theory with Engineering Applications: Nash Bargaining Solution, by Asu Ozdaglar, MIT 2010
