1. Desired Properties
- invariant to coordinate-wise affine transformation
- symmetry-preserving
- efficient
- monotone
2. Problem Statement
We consider a two-person bargaining problem formulated as follows
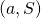 : to every two-person game we associated a pair
: to every two-person game we associated a pair 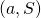 , where
, where  is a point in the plane and
is a point in the plane and 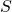 is a subset of the plane.
is a subset of the plane. - The pair
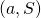 has the following intuitive interpretation:
has the following intuitive interpretation: 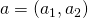 where
where 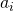 is the level of utility that player
is the level of utility that player 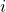 receives if the two players do not cooperate with each other.
receives if the two players do not cooperate with each other. - Every point
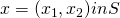 represents the level of utility for players 1 and 2 that can be reached by an outcome of the game which is feasible for the two players when they do cooperate.
represents the level of utility for players 1 and 2 that can be reached by an outcome of the game which is feasible for the two players when they do cooperate.
3. Assumption
- Assumption 1: There is at least one point
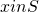 such that
such that 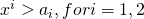 . In other words, bargaining may prove worthwhile for both players.
. In other words, bargaining may prove worthwhile for both players. - Assumption 2:
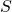 is convex. This is justified under the assumption if two outcomes of the game give raise to points
is convex. This is justified under the assumption if two outcomes of the game give raise to points 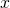 and
and 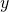 in
in 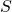 , then randomization of these two outcomes give raise to all convex combinations of
, then randomization of these two outcomes give raise to all convex combinations of 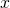 and
and 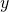 .
. - Assumption 3:
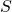 is compact.
is compact. - Assumption 4:
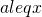 for every
for every 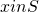 . If this is not the case, we can disregard all the points of
. If this is not the case, we can disregard all the points of 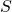 that fail to satisfy this condition because it is impossible that both players will agree to such a solution.
that fail to satisfy this condition because it is impossible that both players will agree to such a solution.
4. Axioms
We let ![]() denote the set of pairs
denote the set of pairs ![]() that satisfying these four conditions, and we call an element in
that satisfying these four conditions, and we call an element in ![]() a bargaining pair.
a bargaining pair.
- Axiom 1: Pareto Optimality
- For every
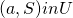 there is no
there is no 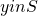 such that
such that 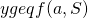 and
and 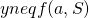 .
. - Axiom 2: Symmetry
- We let
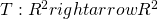 be defined by
be defined by 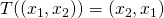 and we require that for every
and we require that for every 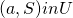 ,
, 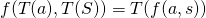 .
. - Axiom 3: Invariance with Respect to Affine Transformation of Utility
- A is an afine transformation of utility if
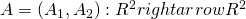 ,
, 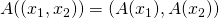 , and the maps
, and the maps 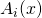 are of the form
are of the form 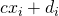 for some positive constant
for some positive constant 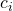 and some constant
and some constant 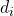 . We require that for such a transformation
. We require that for such a transformation 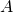 ,
, 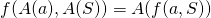 .
.
In addition to the above three axioms, Nash introduced the following
- Axiom of Independence of Irrelavant Alternatives
- If
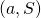 and
and 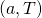 are bargaining pairs such that
are bargaining pairs such that 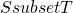 and
and 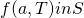 , then
, then 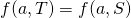 .
. - Interpretation: given a bargaining pair
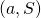 , for every point
, for every point 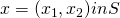 , consider the product
, consider the product 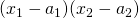 . Then
. Then 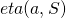 is the unique point in
is the unique point in 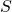 that maximizes this product.
that maximizes this product. - Many objectives are raised to Nash’s axiom of independence of irrelevant alternatives.
We define some notations,
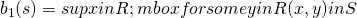
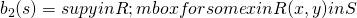
- Let
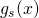 be a function defined for
be a function defined for 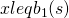 in the following way
in the following way 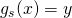 if
if 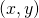 is the Pareto of
is the Pareto of 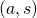 .
. 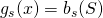 if there is no such
if there is no such  .
.- thus
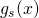 is the maximum player 2 can get if player 1 get at least x.
is the maximum player 2 can get if player 1 get at least x. - By assumption 1 in the definition of a bargaining pair
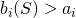 .
. - By the compactness of
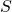 ,
, 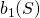 and
and 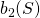 are finite and are attained by points in
are finite and are attained by points in 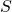 .
. - A pair
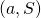 will be called normalized if
will be called normalized if 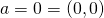 and
and 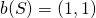 . Clearly every game can be normalized by a unique affine transformation of the utilities.
. Clearly every game can be normalized by a unique affine transformation of the utilities.
Example objective to Nash’s Solution: consider the following two normalized pair ![]() and
and ![]() where
where
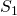 = convex hull,
= convex hull, 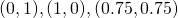 and
and 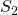 = convex hull,
= convex hull, 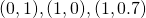
- Nash’s solution for
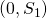 is
is 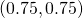 , and
, and 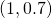 for
for 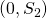 .
. - Limitations pf Nash’s solution: Player 2 has good reasons to demand that he get more in the bargaining pair
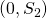 than he does in
than he does in 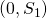 .
.
In order to overcome this limitation, Kalai suggests the following alternative axiom.
Axiom of Monotonicity: If 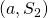 and
and 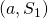 are bargaining pairs such that
are bargaining pairs such that 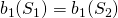 and
and 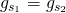 , then
, then 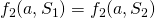 (where
(where 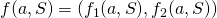 .
.
- This axiom states that if, for every utility level that player 1 may demand, the maximum feasible utility level that player 2 can simultaneously reach is increased, then the utility level assigned to player 2 according to the solution should also be increased.
Theorem: There is one and only one solution, 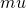 , satisfying the axioms of monotonicity. The function
, satisfying the axioms of monotonicity. The function 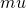 has the following simple representation. For a pair
has the following simple representation. For a pair 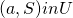 consider the line joining a to be
consider the line joining a to be 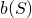 ,
, 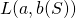 . The maximal element (with partial order of
. The maximal element (with partial order of 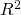 ) of
) of 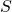 on this line is
on this line is 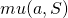 .
.
5. How does it work
- to normalize the utility function of each agent in such a way that it is worth zero at the status quo and one at this agent’s best outcome — given that all others get at least their status quo utility level
- to sharing equally the benefits of cooperation. In other words, this solution equalizes the relative benefit from status quo or equivalently the relative frustration until the shadow optimum.
6. Solution
- Independence of irrelevant alternatives can be substituted with a monotonicity condition. It is the point which maintains the ratios of maximal gains. In other words, if player 1 could receive a maximum of
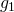 with player 2’s help (and vice versa for
with player 2’s help (and vice versa for 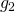 ), then the bargaining solution would yield the point
), then the bargaining solution would yield the point 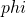 on the Pareto frontier such that
on the Pareto frontier such that 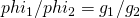 .
.
References
[1] Bargaining problem, wiki
[2] Other solutions to Nash’s bargaining problem, by Ehud Kalai, Meir Smorodinsky, in STOR 1975
