1. Introduction
Definition: the simultaneous buying and selling of securities, currency, or commodities in different markets or in derivative forms in order to take advantage of differing prices for the same asset.
2. Option Pricing
Question:
How to choose x and y:
How to maximize profit:
Key Assumption: There is no limit to buying or selling of options. In practice,
you may only be able to buy, but no sell, for example.
3. Aibitrage Theorem
Definition:
Consider n possible wagers ![]() on m possible outcomes:
on m possible outcomes: ![]() .
.
Let ![]() to be the outcome of wagers i if outcome j occurs.
to be the outcome of wagers i if outcome j occurs.
If ![]() is bet on wager
is bet on wager ![]() , then
, then ![]() is earned if outcome j occurs.
is earned if outcome j occurs.
Arbitrage Theorem:
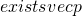 such that
such that 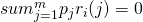 ,
, 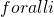
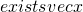 such that
such that 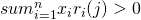
Intuitively,
- First theorem: there is a probability vector such that the expected outcome of every bet is 0, or
- There existing a betting scheme that leads to a sure win.
## TODO: explain more about these two theorem
