1. Motivation
Definition: Let ![]() be Brownian motion with drift coefficient
be Brownian motion with drift coefficient ![]() and variance parameter
and variance parameter ![]() . Let
. Let ![]() . Then
. Then ![]() is geometric Brownian motion.
is geometric Brownian motion.
Motivation: Let ![]() be the price of a stock at time
be the price of a stock at time ![]() (where n is distance); Let
(where n is distance); Let ![]() be the fractional increase/decrease in the price of the stock from time n-1 to time n.
be the fractional increase/decrease in the price of the stock from time n-1 to time n.
We suppose that ![]() are i.i.d. Then
are i.i.d. Then![]()
![]()
The process ![]() looks like a random walk.
looks like a random walk.
2. Property of Geometric Brownian Motion
Proof: ![Rendered by QuickLaTeX.com E[Y(t) | Y(s) = y_s] = E[e^{X(t)} | X(s) = ln y_s]](http://mytechroad.com/wp-content/ql-cache/quicklatex.com-701e5d1e797fb903bd2750dec8a1eed7_l3.png)
= ![Rendered by QuickLaTeX.com E[e^{X(t) - X(s) + X(s)} | X(s) = ln y_s]](http://mytechroad.com/wp-content/ql-cache/quicklatex.com-cbaa4bc6913e4710b685d37a0c9ed632_l3.png)
= ![Rendered by QuickLaTeX.com y_s E[e^{X(t) - X(s)}]](http://mytechroad.com/wp-content/ql-cache/quicklatex.com-8719921d7edc09270eaaf88041d3ce07_l3.png)
- E[Y(t) | Y(s) = y_s] = y_s e^{mu(t-s) + sigma^2(t-s)/2}
Proof: If W ~ 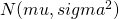 , then
, then 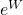 is lognormal with mean
is lognormal with mean ![Rendered by QuickLaTeX.com E[e^W] = e^{mu + sigma^2/2}](http://mytechroad.com/wp-content/ql-cache/quicklatex.com-8f034b090dfb3a6326d07789f19c1cc4_l3.png)
Thus, {X(t) – X(s)} ~![Rendered by QuickLaTeX.com N[mu(t-s), sigma^2(t-s)]](http://mytechroad.com/wp-content/ql-cache/quicklatex.com-fe97cb2671709fb45d594be3e856395c_l3.png) , since
, since 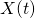 is Brownian motion with drift
is Brownian motion with drift
Thus, {X(t) – X(s)} ~
- Note: if
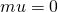 , then
, then ![Rendered by QuickLaTeX.com E[Y(t)|Y(0) = y_0 ] = y_0 e^{sigma^2 t/2}](http://mytechroad.com/wp-content/ql-cache/quicklatex.com-9a556a5f4b14c08ba70ffb8439f32f49_l3.png) . Thus
. Thus ![Rendered by QuickLaTeX.com E[Y(t)]](http://mytechroad.com/wp-content/ql-cache/quicklatex.com-81766f2a95bfc8f5b83bea45159b759f_l3.png) is increasing even though the jump process with
is increasing even though the jump process with 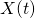 is symmetric
is symmetric
3. Example
Question: You invest 1000 dollars in the stock market. Suppose that the stock market can be modeled using geometric Brownian motion with an average daily return of 0.03% and a standard deviation of 1.02%. what is the probability that your money increases after 1 year (260 business days?) 10 years? 30 years?
Question: You invest 1000 dollars in the stock market. Suppose that the stock market can be modeled using geometric Brownian motion with an average daily return of 0.03% and a standard deviation of 1.02%. what is the probability that your money increases after 1 year (260 business days?) 10 years? 30 years?
Answer: Let ![]() , where
, where ![]() is standard Brownian Motion.
is standard Brownian Motion.
Let ![]() where
where ![]() is standard Brownian motion,
is standard Brownian motion, ![]() is Brownian motion with drift, and
is Brownian motion with drift, and ![]() is geometric Brownian motion.
is geometric Brownian motion.
![]()
= ![]()
= ![]()
= ![]()
= ![]()
= ![]()
