Monthly Archives: February 2016

Return-to-libc attack

Posted on by
Reply

A “return-to-libc” attack is an attack that is usually starting with a buffer overflow in which a subroutine return address on a call stack is replaced by an address of a subroutine that is already present in the process’s executable memory, bypassing the NX bit feature (if present) and ridding the attacker of the need to inject their own code.

On POSIX-compliant operating system the C standard library is commonly used to provide a standard runtime environment for programs writing in the C programming language. Although the attacker could make the code return anywhere, libc is the most likely target, as it is almost always linked to the program, and it provides useful calls for an attacker (such as the system function used to execute shell commands)

Reference
[1] https://en.wikipedia.org/wiki/Return-to-libc_attack

How to test network bandwidth between two machines

Posted on by
Reply

http://askubuntu.com/questions/7976/how-do-you-test-the-network-speed-betwen-two-boxes

I use iperf. It’s a client server arrangement in that you run it in server mode at one end and connect to its from another computer on the other side of the network.
One both machines run:
sudo apt-get install iperf
Then on Computer A (Server):
iperf -s
And on Computer B (Client):
iperf -c <address of Computer A>

Install latest eclipse in Linux

Posted on by
Reply

Guidance from: http://askubuntu.com/questions/26632/how-to-install-eclipse

How to install Eclipse 4.2 on Ubuntu 12.04
Since the Eclipse packages in the Ubuntu repositories are out of date, if we want to install latest releases, we are going to have to do it manually. You can just download the tar.gz file fromeclipse.org.
  1. Download Eclipse. I got eclipse-jee-juno-SR1-linux-gtk.tar.gz
  2. Extract it by executing a command line
    tar -xzf eclipse-jee-juno-SR1-linux-gtk.tar.gz
    Or with Archive Manager extraction.
  3. Move extracted eclipse folder to /opt/ folder
    mv eclipse /opt/
    sudo chown -R root:root /opt/eclipse
    sudo chmod -R +r /opt/eclipse
  4. Create an eclipse executable in your user path
    sudo touch /usr/bin/eclipse
    sudo chmod 755 /usr/bin/eclipse
    Create a file named eclipse in /usr/bin/ with your preferred editor (nano, gedit, vi…)
    Copy this into it
    #!/bin/sh    
    export ECLIPSE_HOME="/opt/eclipse"
    ECLIPSE_HOME/eclipse*
    And save the file
  5. Create a Gnome menu item
    Create a file named eclipse.desktop in /usr/share/applications/ with your preferred editor (nano, gedit, vi…)
    Copy this into it
    [Desktop Entry]
    Encoding=UTF-8
    Name=Eclipse
    Comment=Eclipse IDE
    Exec=eclipse
    Icon=/opt/eclipse/icon.xpm
    Terminal=false
    Type=Application
    Categories=GNOME;Application;Development;
    StartupNotify=true
    And save the file
  6. Launch Eclipse
    /opt/eclipse/eclipse -clean &
  7. Now you can Lock Eclipse to the launcher bar by clicking right button on Lock to Laucher

bin and ball

Posted on by
Reply

Lemma

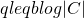
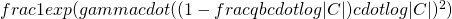
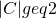
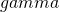
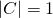
[1] Consider a process that throws balls uniformly at random into b bins and let C be a subset of these bins. If the process throws q leq b log|C| balls, then the probability that each bin in C has at least one ball is at most frac{1}{exp(gamma cdot ((1 - frac{q}{b cdot log|C|}) cdot log|C|)^2)} if |C| geq 2, where gamma is some constant strictly less than 1. If |C| = 1, then the probability is at most 1 - (1/4)^{q/b}.

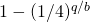
Comment: conpon analysis + chernoff bound

Lemma

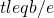
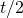
[1] Consider a process that throws t balls into b bins uniformly at random. if t leq b/e, then the probability that there are at most t/2 occupied bins is at most 2^{-t/2}.

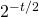
Lemma

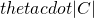
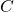
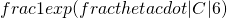
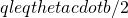
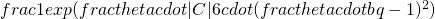
[1] Consider a process that throws balls uniformly at random into b bins and let C be a subset of these bins. If the process throws q balls, then the probability that at least theta cdot |C| of the bins in C have at least one ball is at most frac{1}{exp(frac{theta cdot |C|}{6})} if q leq theta cdot b /2; and at most frac{1}{exp(frac{theta cdot |C|}{6} cdot (frac{theta cdot b}{q}-1)^2)} if theta cdot b/2 < q < theta cdot b. 

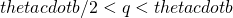
Reference

[1] Co-Location-Resistant Clouds, by Yossi Azar et al. in CCSW 2014