1. Introduction
- At any time s,
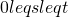 , you can buy or sell shares of stock for
, you can buy or sell shares of stock for 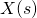
- At time
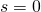 , there are N options available. The cost of option
, there are N options available. The cost of option  is
is 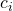 per option which allows you to purchase
per option which allows you to purchase 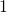 share at time
share at time 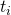 for price
for price 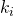 .
.
2. Analyze Bet 0: Purchase 1 share of stock at time s
Choose ![]() such that
such that ![]()
Then ![]() .
.
Thus the expected present value of the stock at t equals the present value of the stock when it is purchased at time s. That is, the discount rate exactly equals to the expected rate of the stock returns.
3. Analyze Bet i: Purchase 1 share of option i (at time s =0)
First, we drop the subscript i to simplify notation.
Expected present value of the return on this bet is
![]()
= ![]()
Setting this equal to zero implies that![]()
= ![]()
![]() has value 0 when
has value 0 when ![]() , i.e., when
, i.e., when ![]()
Thus the integral becomes![]()
= ![]()
Now, apply a change of variables:![]() , i.e.,
, i.e., ![]()
4. Summary
- If we suppose that the stock price follow geometric Brownian motion and we choose the option costs according to the above formula, then the expected outcome of every bet is 0.
- Note: the stock price does not actually need to follow geometric Brownian motion. We are saying that if stock price follow Brownian motion, then the expected outcome of very bet would be 0, so no arbitrage exists.
- When
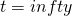 , cost of option is
, cost of option is 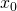
- When
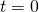 , cost of option is
, cost of option is 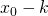
- As t increases, c increases
- As k increases, c decreases
- As
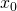 increases, c increases
increases, c increases - As
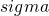 increase, c increase (assuming
increase, c increase (assuming 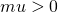 )
) - As
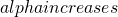 , c decreases
, c decreases

 X(s) = x | X(t) = B
X(s) = x | X(t) = B X(t)
X(t)