logic expression conversion in ILP

Posted on February 9, 2016 by admin

http://cs.stackexchange.com/questions/12102/express-boolean-logic-operations-in-zero-one-integer-linear-programming-ilp

bin and ball

Posted on February 6, 2016 by admin

Lemma

[1] Consider a process that throws balls uniformly at random into b bins and let C be a subset of these bins. If the process throws $q leq b log|C|$ balls, then the probability that each bin in C has at least one ball is at most $frac{1}{exp(gamma cdot ((1 - frac{q}{b cdot log|C|}) cdot log|C|)^2)}$ if $|C| geq 2$ , where $gamma$ is some constant strictly less than 1. If $|C| = 1$ , then the probability is at most $1 - (1/4)^{q/b}$ .

Comment: conpon analysis + chernoff bound

Lemma

[1] Consider a process that throws t balls into b bins uniformly at random. if $t leq b/e$ , then the probability that there are at most $t/2$ occupied bins is at most $2^{-t/2}$ .

Lemma

[1] Consider a process that throws balls uniformly at random into b bins and let C be a subset of these bins. If the process throws q balls, then the probability that at least $theta cdot |C|$ of the bins in $C$ have at least one ball is at most $frac{1}{exp(frac{theta cdot |C|}{6})}$ if $q leq theta cdot b /2$ ; and at most $frac{1}{exp(frac{theta cdot |C|}{6} cdot (frac{theta cdot b}{q}-1)^2)}$ if $theta cdot b/2 < q < theta cdot b$ .

Reference

[1] Co-Location-Resistant Clouds, by Yossi Azar et al. in CCSW 2014

Online Hiring Problem

Posted on January 18, 2016 by admin

Problem

If there are n candidates, and we do not want to interview all candidates to find the best one. We also do not wish to hire and fire as we find better and better candidates.

Instead, we are willing to settle for a candidate who is close to the best, in exchange of hiring exactly once.

For each interview we must either immediately offer the position to the applicant or immediately reject the applicant.

What is the trade-off between minimizing the amount of interviewing and maximizing the quality of the candidate hired?

Code

Analysis

We analysis in the following to determine the best value of k that maximize the probability we hire the best candidate. In the analysis, we assume the index starts with 1 (rather than 0 as shown in the code).

Let $B_i$ be the event that the best candidate is the $i$ -th candidate.
Let $O_i$ be the event that none of the candidate in position $k+1$ to $i-1$ is chosen.
Let $S_i$ be the event that we hire the best candidate when the best candidate is in the $i$ -th position.

We have $Pr(S_i ) = Pr (B_i cup O_i) = Pr(B_i) cdot Pr(O_i)$ since $B_i$ and $O_i$ are independent events.

$Pr(S_i) = sum^n_{i=k+1} Pr(S_i)$
$= sum^n_{i=k+1} frac{1}{n} cdot frac{k}{n-i}$
$= frac{k}{n} sum^n_{i=k+1} frac{1}{i-1}$
$leq frac{k}{n} cdot (ln n - ln k)$

Setting this derivative equal to 0, we see that we maximize the probability, i.e., when $k = n/e$ , we have the probability at least $1/e$ .

Reference
[1] Introduction to Algorithms, CLSR

随机过程总结

Posted on October 5, 2015 by admin

参开资料：
http://www.zhihu.com/question/23527615

随机过程一般理论
– 概率论、随机过程的测度论基础：probability space、convergence theory、limit theory、martingale theory
– Markov process
– stochastic integral
– stochastic differential equations
– semimartingale theory

数学金融：
– stochastic integrals
– stochastic differential equations (SDE)
– semimartingale
– Ito process
– Levy process：解决ruin问题
– Brownian motion

Average Age of Renewal Process

Posted on December 12, 2014 by admin

1. Definition

Let 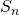$S_n$ be the n-th renewal
Then 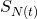$S_{N(t)}$ = time of the last renewal (prior to time t)
Let $A(t) = t - S_{N(t)}$

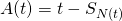
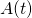$A(t)$ is called the age of the renewal process
Interpretation: A(t) is the time since last renewal

2. Average Age of Renewal Process

What is $R_n$ ? $R_n = int^{S_n}_{S_{n-1}} A(t) dt$
$R_n$ is the area under the curve for one cycle
so $E(R_n)) = E[(X_n)^2/2] = E[X^2_n]/2$
Thus the long-run average of the process is

$frac{E[R_n]}{E[X_n]} = frac{E[X^2_n]}{2E[X_n]}$

Renewal-Reward Process

Posted on December 11, 2014 by admin

1. Definition

let 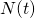$N(t)$ be a renewal process
Let 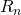$R_n$ = reward earned at 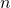$n$ -th renewal
Assume 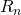$R_n$ are i.i.d, but can depend on 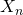$X_n$ (length of the 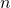$n$ -th cycle)

Then $R(t) = sum^{N(t)}_{n=1} R_n$ is a renewal reward process.

Intuitive explanation: $R(t)$ = cumulative reward earned up to time t

2. Renewal Reward Theorem

Proposition 7.3

$lim_{t to infty} frac{R(t)}{t} = frac{E[R_n]}{E[X_n]}$
$lim_{t to infty} frac{E[R(t)]}{t} = frac{E[R_n]}{E[X_n]}$

Provided $E[R_n] < infty, E[X_n] < infty$

3. Example: Inventory Problem

Problem:

Solution:

Reversible Markov Chain

Posted on December 11, 2014 by admin

1. Definition

Let $X_1, X_2, cdots$ be a Markov chain with transition probabilities $P_{ij}$ .

$P_{ij} = Pr{X_{n+1} = j| X_n = i}$

E.g. A sample realization is 1, 2, 3, 4, 5

Let $X_n, x_{n-1}, cdots$ be the same sequence in reverse, i.e. $cdots, 5, 4, 3, 2, 1, cdots$

Let $Q_{ij}$ be the transition probabilities of the reversed process. That is
$Q_{ij} = Pr{X_{n-1} = j |X_n = i}$
= $frac{Pr{X_{n-1} =j, X_n = i}}{Pr{X_n = i}}$
= $frac{Pr{X_{n-1} = j} Pr{X_n =i | X_{n-1} = j}}{Pr{X_n = i}}$
= $frac{Pr{X_{n-1} = j} P_{ji}}{Pr{X_n = i}}$

2. Conclusion

In the steady state, assuming the limiting probabilities exist, we have
$Q_{ij} = frac{pi_j P_{ji}}{pi_i}$ or $pi_i Q_{ij} = pi_j Q_{ji}$

The above equation is saying that the rate of transmissions from i to j in the reversed chain is equal to the rate of transitions from j to i in the forward chain.

A DTMC is time reversible if $Q_{ij} = P_{ij}$

Markov Chain — Birth-Death Processes

Posted on December 11, 2014 by admin

– Stochastic Course Notes

1. Definition

2. Expected Time to State n

3. Example

Markov Chain — Branching Process

Posted on December 11, 2014 by admin

– Stochastic Course Notes

1. Definition

Consider a population

Each individual produces j new offspring each period with probability 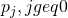$p_j, j geq 0$ . Key assumption: This distribution is constant over time.
Assume that 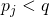$p_j < q$ for all j (i.e., the problem is not deterministic)
Let 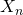$X_n$ be the size of the population at period n