1. Definition
Let 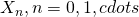 be a stochastic process, taking on a finite or countable number of values.
be a stochastic process, taking on a finite or countable number of values.
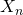 is a DTMC if it has the Markov property: Given the present, the future is independent of the past
is a DTMC if it has the Markov property: Given the present, the future is independent of the past
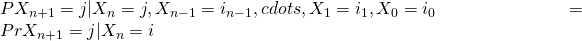
We define 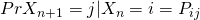 , since
, since 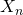 has the stationary transition probabilities, this probability is not depend on n.
has the stationary transition probabilities, this probability is not depend on n.
Transition probabilities satisfy 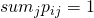
2. n Step transition Probabilities
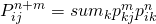
Proof:
3. Example: Coin Flips
4. Limiting Probabilities
Theorem: For an irreducible, ergodic Markov Chain, 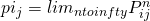 exists and is independent of the starting state i. Then
exists and is independent of the starting state i. Then 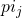 is the unique solution of
is the unique solution of 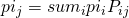 and
and 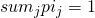 .
.
Two interpretation for 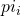
- The probability of being in state i a long time into the future (large n)
- The long-run fraction of time in state i
Note:
- If Markov Chain is irreducible and ergodic, then interpretation 1 and 2 are equivalent
- Otherwise,
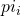 is still the solution to
is still the solution to 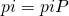 , but only interpretation 2 is valid.
, but only interpretation 2 is valid.
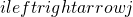 ) if i is reachable from j and j is reachable from i. (Note: a state i always communicates with iteself)
) if i is reachable from j and j is reachable from i. (Note: a state i always communicates with iteself)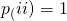
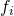 : be the probability that, starting in state i, the process returns (at some point) to the sate i
: be the probability that, starting in state i, the process returns (at some point) to the sate i
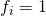 . There are two types of reurrent states
. There are two types of reurrent states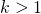 where k is the smallest number such that all paths leading from state i back to state i has a multiple of k transitions
where k is the smallest number such that all paths leading from state i back to state i has a multiple of k transitions