1. Introduction
Motivation: Find the cost of buying options to prevent arbitrage opportunity.
Definition: Let
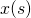
be the price of a stock at time s, considered on a time horizon
![Rendered by QuickLaTeX.com s in [0,t]](http://mytechroad.com/wp-content/ql-cache/quicklatex.com-a762adbae0fb6065ce545731c1dcb638_l3.png)
. The following actions are available:
Approach: By the arbitrage theorem, this requires finding a probability measure so that each bet has zero expected pay off.
We try the following probability measure on
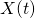
: suppose that
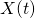
is geometric Brownian motion. That is,
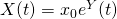
, where
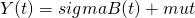
.
2. Analyze Bet 0: Purchase 1 share of stock at time s
Now, we consider a discount factor
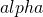
. Then, the expected present value of the stock at time t is
![Rendered by QuickLaTeX.com E[e^{-alpha t} X(t) | X(s)] = e^{-alpha t} X(s) e { mu/(t-s) + frac{sigma^2(t-s)}{2}}](http://mytechroad.com/wp-content/ql-cache/quicklatex.com-12ddc47252af565aed0785998a1baf5e_l3.png)
Choose 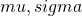 such that
such that 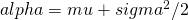
Then ![Rendered by QuickLaTeX.com E[e^{-alpha t} X(t) | X(s)] = e^{-alpha t} X(s) e^{-alpha(t-s)} = e^{-alpha s} X(s)](http://mytechroad.com/wp-content/ql-cache/quicklatex.com-5f9bdae01a64793ac51fed04f2eed82f_l3.png) .
.
Thus the expected present value of the stock at t equals the present value of the stock when it is purchased at time s. That is, the discount rate exactly equals to the expected rate of the stock returns.
3. Analyze Bet i: Purchase 1 share of option i (at time s =0)
First, we drop the subscript i to simplify notation.
Expected present value of the return on this bet is
![Rendered by QuickLaTeX.com - c + E[max (e^{alpha t} X(t)- k), 0]](http://mytechroad.com/wp-content/ql-cache/quicklatex.com-a9cb06d5f71316f190c3485fd436505c_l3.png)
= ![Rendered by QuickLaTeX.com -c + E[e^{-alpha t} (X(t) - k)^+]](http://mytechroad.com/wp-content/ql-cache/quicklatex.com-0e6064bae2e4f52212c1a87c8be915e9_l3.png)
Setting this equal to zero implies that
![Rendered by QuickLaTeX.com ce^{alpha t} = E[ (X(t) - k)^+] = E[(x_0 e^{Y(t)} - k)^+]](http://mytechroad.com/wp-content/ql-cache/quicklatex.com-fc5742e0bd281ec47bddd20ecce7594a_l3.png)
= 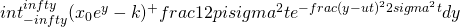
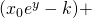 has value 0 when
has value 0 when 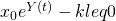 , i.e., when
, i.e., when 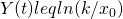
Thus the integral becomes
![Rendered by QuickLaTeX.com ce^{alpha t} = E[ (X(t) - k)^+] = E[(x_0 e^{Y(t)} - k)^+]](http://mytechroad.com/wp-content/ql-cache/quicklatex.com-fc5742e0bd281ec47bddd20ecce7594a_l3.png)
= 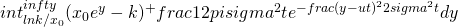
Now, apply a change of variables:
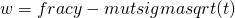 , i.e.,
, i.e., 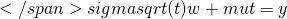
4. Summary
No arbitrage exists if we find costs and a probability distribution such that expected outcome of every bet is 0.
- If we suppose that the stock price follow geometric Brownian motion and we choose the option costs according to the above formula, then the expected outcome of every bet is 0.
- Note: the stock price does not actually need to follow geometric Brownian motion. We are saying that if stock price follow Brownian motion, then the expected outcome of very bet would be 0, so no arbitrage exists.
A few sanity checks
- When
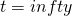 , cost of option is
, cost of option is 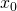
- When
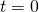 , cost of option is
, cost of option is 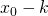
- As t increases, c increases
- As k increases, c decreases
- As
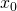 increases, c increases
increases, c increases
- As
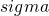 increase, c increase (assuming
increase, c increase (assuming 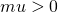 )
)
- As
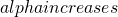 , c decreases
, c decreases
 : Infinite number of servers
: Infinite number of servers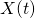 be the number of customers who have completed service by time t
be the number of customers who have completed service by time t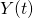 be the number of customers who are being served at time t
be the number of customers who are being served at time t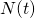 be the total number of customers who have arrived by time t
be the total number of customers who have arrived by time t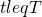 is
is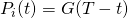
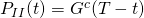
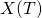 is a Poisson random variable with mean
is a Poisson random variable with mean 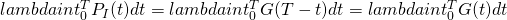 .
.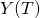 is a Poisson random variable with mean
is a Poisson random variable with mean 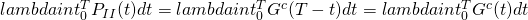
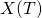 and
and 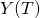 are independent
are independent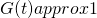 for large t. Therefore,
for large t. Therefore, 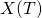 is a Poisson random variable with mean
is a Poisson random variable with mean 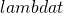
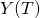 is a Poisson random variable with mean
is a Poisson random variable with mean ![Rendered by QuickLaTeX.com lambda int^T_0 G^ct)dt = lambda E[G]](http://mytechroad.com/wp-content/ql-cache/quicklatex.com-2c5d36fa13d7d0d546ab1022413e9709_l3.png)
